Math.atan2()

¥Syntax

Math.atan2(y, x)

¥Parameters

y

点的 y 坐标。

x

点的 x 坐标。

¥Return value

正 x 轴与从 (0, 0) 到点 (x, y) 的射线之间的角度（以弧度为单位，介于 -π 和 π 之间）。

¥The angle in radians (between -π and π, inclusive) between the positive x-axis and the ray from (0, 0) to the point (x, y).

¥Description

Math.atan2() 方法测量正 x 轴和点 (x, y) 之间的逆时针角度 θ（以弧度为单位）。请注意，此函数的参数首先传递 y 坐标，然后传递 x 坐标。

¥The Math.atan2() method measures the counterclockwise angle θ, in radians, between the positive x-axis and the point (x, y). Note that the arguments to this function pass the y-coordinate first and the x-coordinate second.

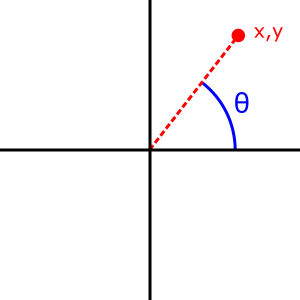
Math.atan2() 传递单独的 x 和 y 参数，而 Math.atan() 传递这两个参数的比率。Math.atan2(y, x) 在以下情况下与 Math.atan(y / x) 不同：

¥Math.atan2() is passed separate x and y arguments, while Math.atan() is passed the ratio of those two arguments. Math.atan2(y, x) differs from Math.atan(y / x) in the following cases:

此外，对于第二和第三象限 (x < 0) 中的点，Math.atan2() 将输出小于 或大于

¥In addition, for points in the second and third quadrants (x < 0), Math.atan2() would output an angle less than $-\frac{\pi}{2}$ or greater than $\frac{\pi}{2}$.

因为 atan2() 是 Math 的静态方法，所以你始终将其用作 Math.atan2()，而不是用作你创建的 Math 对象的方法（Math 不是构造函数）。

¥Because atan2() is a static method of Math, you always use it as Math.atan2(), rather than as a method of a Math object you created (Math is not a constructor).

¥Examples

¥Using Math.atan2()

Math.atan2(90, 15); // 1.4056476493802699
Math.atan2(15, 90); // 0.16514867741462683

¥Difference between Math.atan2(y, x) and Math.atan(y / x)

以下脚本打印在 Math.atan2(y, x) 和 Math.atan(y / x) 之间产生差异的所有输入。

¥The following script prints all inputs that produce a difference between Math.atan2(y, x) and Math.atan(y / x).

const formattedNumbers = new Map([
  [-Math.PI, "-π"],
  [(-3 * Math.PI) / 4, "-3π/4"],
  [-Math.PI / 2, "-π/2"],
  [-Math.PI / 4, "-π/4"],
  [Math.PI / 4, "π/4"],
  [Math.PI / 2, "π/2"],
  [(3 * Math.PI) / 4, "3π/4"],
  [Math.PI, "π"],
  [-Infinity, "-∞"],
  [Infinity, "∞"],
]);

function format(template, ...args) {
  return String.raw(
    { raw: template },
    ...args.map((num) =>
      (Object.is(num, -0)
        ? "-0"
        : formattedNumbers.get(num) ?? String(num)
      ).padEnd(5),
    ),
  );
}

console.log(`| x     | y     | atan2 | atan  |
|-------|-------|-------|-------|`);

for (const x of [-Infinity, -1, -0, 0, 1, Infinity]) {
  for (const y of [-Infinity, -1, -0, 0, 1, Infinity]) {
    const atan2 = Math.atan2(y, x);
    const atan = Math.atan(y / x);
    if (!Object.is(atan2, atan)) {
      console.log(format`| ${x} | ${y} | ${atan2} | ${atan} |`);
    }
  }
}

输出是：

¥The output is:

| x     | y     | atan2 | atan  |
|-------|-------|-------|-------|
| -∞    | -∞    | -3π/4 | NaN   |
| -∞    | -1    | -π    | 0     |
| -∞    | -0    | -π    | 0     |
| -∞    | 0     | π     | -0    |
| -∞    | 1     | π     | -0    |
| -∞    | ∞     | 3π/4  | NaN   |
| -1    | -∞    | -π/2  | π/2   |
| -1    | -1    | -3π/4 | π/4   |
| -1    | -0    | -π    | 0     |
| -1    | 0     | π     | -0    |
| -1    | 1     | 3π/4  | -π/4  |
| -1    | ∞     | π/2   | -π/2  |
| -0    | -∞    | -π/2  | π/2   |
| -0    | -1    | -π/2  | π/2   |
| -0    | -0    | -π    | NaN   |
| -0    | 0     | π     | NaN   |
| -0    | 1     | π/2   | -π/2  |
| -0    | ∞     | π/2   | -π/2  |
| 0     | -0    | -0    | NaN   |
| 0     | 0     | 0     | NaN   |
| ∞     | -∞    | -π/4  | NaN   |
| ∞     | ∞     | π/4   | NaN   |

¥See also

• Math.acos()
• Math.asin()
• Math.atan()
• Math.cos()
• Math.sin()
• Math.tan()